Compound Interest Calculator

Principal Amount:

Annual Interest Rate (%):

Time (years):

Calculate

A Comprehensive Guide: Compound Interest Calculator

Introduction

Understanding the concept of compound interest is your ticket to achieving your financial goals faster and more efficiently. In this comprehensive guide, we’ll take you through everything you need to know about compound interest and how it can work for you.

Section 1: What is Compound Interest?

Define compound interest.

Compound interest is the magic that happens when your money earns interest on both the initial amount you invested or borrowed (the principal) and the interest that has already accumulated. It’s a stark contrast to simple interest, which only calculates interest on the principal. To grasp this concept, let’s delve into some examples.

The difference between simple interest and compound interest

Imagine you borrowed $100 at a 10% annual interest rate for two years. With simple interest, you’d owe $20 at the end of those two years. But with compound interest, your debt would grow to $21, thanks to the interest compounding on both the principal and the interest accrued.

Section 2: How Compound Interest Works

How compound interest is calculated?

Now, let’s see how compound interest can work its magic in real life. Consider a young individual who invests $1,000 in the stock market at a 10% annual return rate at the age of 20. By the time they retire at 65, their investment will have grown to a staggering $72,890—approximately 73 times their initial investment!

The exponential growth of compound interest

The exponential growth of compound interest is a fundamental concept in finance and investing that demonstrates the remarkable power of time and consistent contributions. It’s the process by which your money grows not just linearly but exponentially over time, thanks to the compounding effect. Let’s delve into this concept and understand why it’s so important:

1. Compounding Principle:

• Compound interest involves earning interest not only on the initial principal amount but also on the interest that has previously accumulated. In other words, you earn interest on your interest.

2. Exponential Growth Over Time:

• At the heart of the exponential growth of compound interest is the idea that as interest is added to the principal, the total amount grows larger. As this larger sum continues to earn interest, the growth accelerates.
• The growth is exponential because it follows an exponential function, where the rate of growth increases as the investment period extends.

3. Time Is Your Greatest Ally:

• Compound interest’s most significant advantage is the effect of time. The longer your money remains invested, the more significant the exponential growth becomes.
• This concept is often referred to as the “time value of money.” It means that a dollar invested today is worth more than a dollar invested in the future because it has more time to compound and grow.

4. Consistency Amplifies Growth:

• Regular contributions or investments, coupled with compound interest, amplify the exponential growth effect. When you consistently add money to your investment or savings over time, you’re increasing the principal amount that’s compounding.
• For example, in a retirement account, making regular contributions allows you to benefit not only from the compounding of your initial investment but also from the compounding of each subsequent contribution.

5. Illustrating the Benefits:

• To showcase the power of exponential growth, consider this example: If you invest $1,000 at a 10% annual return rate, after one year, you’ll have $1,100. However, after ten years, you’ll have approximately $2,593.74. Notice how the growth becomes more significant as time goes on.

6. Impact on Wealth Accumulation:

• Exponential growth is a driving force behind wealth accumulation and financial security. It’s why long-term investing, such as saving for retirement or building an investment portfolio, is so effective.
• Compound interest allows you to turn relatively modest initial investments into substantial sums of money over time.

7. Compounding Frequencies:

• The frequency of compounding plays a role in the extent of exponential growth. The more frequent the compounding (e.g., monthly instead of annually), the faster your money grows.

A real-life example of investing in the stock market to showcase the benefits of compound interest

Let’s explore a real-life example of investing in the stock market to illustrate the remarkable benefits of compound interest.

Scenario:

Imagine two individuals, Alex and Ben, both aged 25, deciding to invest in the stock market for their retirement. They both start with an initial investment of $10,000. Alex chooses to invest a lump sum of $10,000 and leave it untouched until retirement at age 65, while Ben decides to invest $1,000 annually from age 25 to 65.

Alex’s Strategy:

Alex invests $10,000 at the age of 25 and doesn’t make any additional contributions. Over the years, his investment has grown based on the historical average annual return of the S&P 500, which is approximately 10% (compounded annually).

Ben’s Strategy:

Ben also starts with an initial investment of $10,000 at age 25, but he contributes an additional $1,000 to his investment every year until age 65. Like Alex, Ben’s investments also grow at an average annual return of 10% (compounded annually).

Results:

Let’s compare the outcomes for both Alex and Ben at age 65:

Alex’s Investment:

• Initial Investment: $10,000
• Annual Contribution: $0
• Average Annual Return: 10% (compounded annually)
• Time Period: 40 years

Using the compound interest formula:
At = A0(1 + r)^n

At = $10,000(1 + 0.10)^40
At ≈ $452,593.57

At age 65, Alex’s initial $10,000 investment would have grown to approximately $452,593.57.

Ben’s Investment:

• Initial Investment: $10,000
• Annual Contribution: $1,000
• Average Annual Return: 10% (compounded annually)
• Time Period: 40 years

Ben’s contributions and returns can be more complex to calculate manually, but using financial calculators or spreadsheet software, we can determine that Ben’s investment would grow to approximately $1,550,058.77 by age 65.

Comparison:

• Alex, with a single $10,000 investment, ends up with around $452,593.57.
• Ben, with annual contributions of $1,000, ends up with approximately $1,550,058.77.

The power of compound interest is evident in this comparison. Despite starting with the same initial investment, Ben, who consistently added to his investment over time, amassed significantly more wealth by the time they both reached retirement age. Compound interest allowed his contributions to grow exponentially over the years.

This example illustrates how regular contributions, coupled with the magic of compound interest, can lead to substantial wealth accumulation over the long term, making it a compelling strategy for retirement planning and achieving financial goals.

Section 3: Different Compounding Frequencies

How compounding frequency impacts interest calculations

Understanding how often interest compounds is essential. Interest can compound annually, monthly, or even continuously. The frequency impacts how much interest you’ll owe or earn. For instance, a 10% interest rate compounded semi-annually is equivalent to a 10.25% interest rate compounded annually. Lenders often prefer presenting interest rates compounded more frequently to make them appear lower.

Examples of different compounding periods include annual, monthly, and continuous.

Let’s explore examples of different compounding periods, including annual, monthly, and continuous compounding, to understand how they affect the growth of an investment or the interest on a loan.

Annual Compounding:
Annual compounding means that interest is calculated and added to the principal once a year. Here’s an example:

Suppose you invest $1,000 at a 5% annual interest rate with annual compounding. After one year, your investment would grow to:

A = $1,000 * (1 + 0.05)^1 = $1,050

After two years, it would be:

A = $1,000 * (1 + 0.05)^2 = $1,102.50

Monthly Compounding:
Monthly compounding involves calculating and adding interest to the principal every month. Let’s use the same initial investment and interest rate:

If you invest $1,000 at a 5% annual interest rate with monthly compounding, you divide the annual rate by 12 (the number of months in a year) and calculate the monthly interest rate:

Monthly Interest Rate = 5% / 12 = 0.4167%

After one month, your investment would grow to:

A = $1,000 * (1 + 0.004167)^1 ≈ $1,004.17

After two months:

A = $1,004.17 * (1 + 0.004167)^1 ≈ $1,008.34

Continuous Compounding:
Continuous compounding represents the extreme end of compounding, where interest is calculated and added continuously, instant by instant. The formula for continuous compounding is:

A = P * e^(rt)

Where:

• A is the final amount
• P is the principal
• e is Euler’s constant (approximately 2.71828)
• r is the annual interest rate
• t is the time in years

Let’s say you invest $1,000 at a 5% annual interest rate with continuous compounding for one year.

A = $1,000 * 2.71828^(0.05 * 1) ≈ $1,051.27

As you can see, with continuous compounding, your investment grows slightly more than with monthly or annual compounding.

In summary, the compounding frequency affects the growth of an investment or the interest on a loan. The more frequent the compounding, the higher the final amount or interest accrued. Continuous compounding, while not commonly used in practice, represents the theoretical limit of how much an investment can grow over time.

Section 4: Compound Interest Formulas

Basic compound interest formulas.

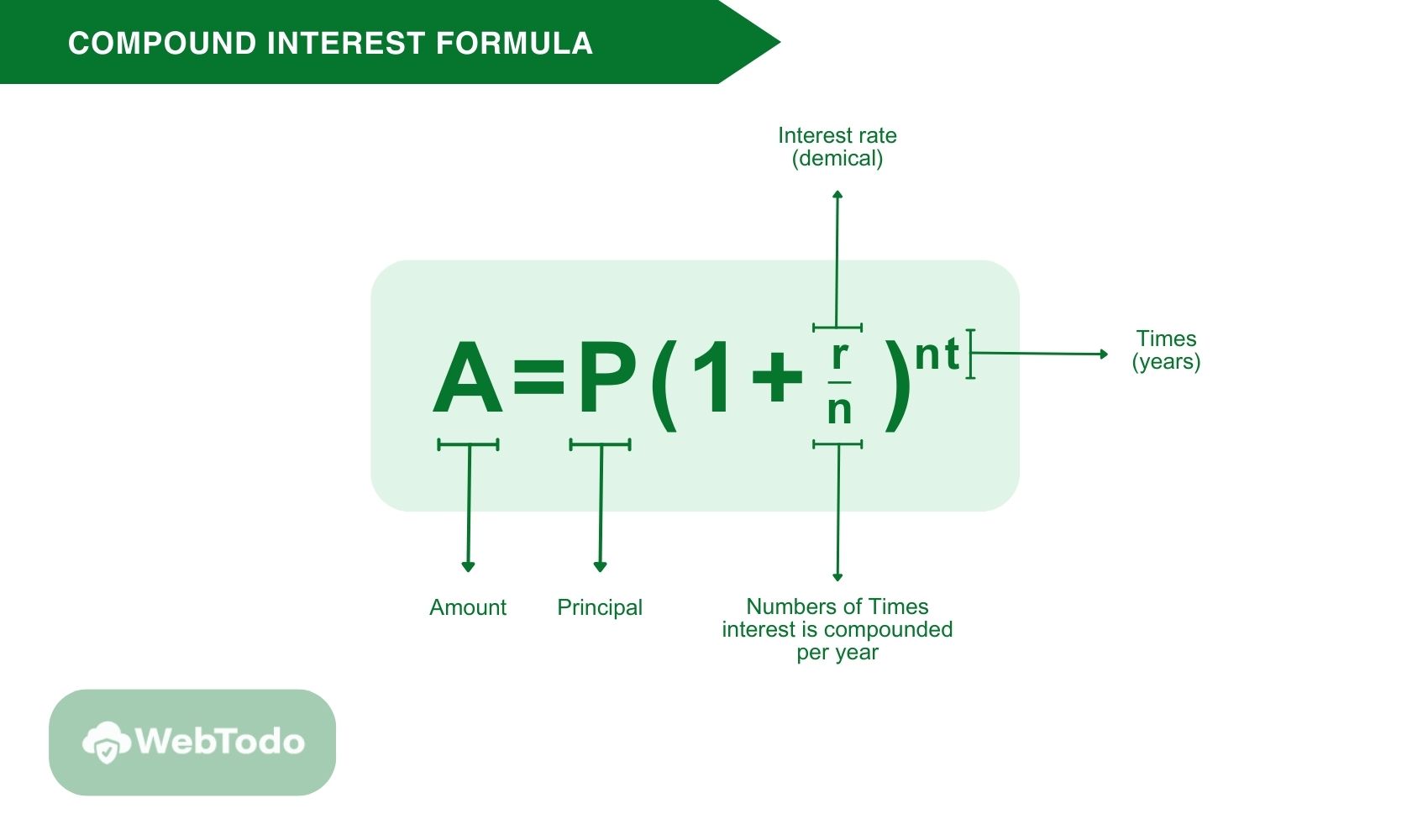
Feeling a bit overwhelmed by the math behind compound interest? Don’t worry; we’ve got you covered. The basic compound interest formula is:

[A__t = A_₀(1 + r)^n]

Explain how to calculate compound interest for different compounding frequencies.

We’ll walk you through different formulas for various compounding frequencies and provide step-by-step examples to make it crystal clear.

Certainly! Let’s use the compound interest formulas to calculate the final amount for different scenarios.

Basic Compound Interest Formula:
The basic formula for compound interest is:

[A_t = A_0(1 + r)^n]

Where:

• (A_t) is the final amount
• (A_0) is the initial amount (principal)
• (r) is the annual interest rate
• (n) is the number of compounding periods, usually expressed in years

Example 1: Annual Compounding:
Suppose you invest $5,000 at an annual interest rate of 8% for 5 years, with annual compounding. Using the formula:

[A_t = $5,000 \times (1 + 0.08)^5]

Calculating:

[A_t = $5,000 \times (1.08)^5 \approx $7,317.49]

So, after 5 years of annual compounding, your investment would grow to approximately $7,317.49.

Example 2: Monthly Compounding:
Now, let’s consider the same initial investment of $5,000 at an annual interest rate of 8%, but this time with monthly compounding. First, we need to adjust the interest rate and the number of compounding periods.

Monthly Interest Rate = 8% / 12 months ≈ 0.006667 (rounded to 6 decimal places)
Number of Compounding Periods (months) = 5 years * 12 months = 60 months

Using the formula:

[A_t = $5,000 \times (1 + 0.006667)^{60}]

Calculating:

[A_t = $5,000 \times (1.006667)^{60} \approx $7,374.49]

With monthly compounding, your investment would grow to approximately $7,374.49 after 5 years.

Example 3 – Continuous Compounding:
In continuous compounding, we use the formula:

[A_t = A_0e^{rt}]

Where:

• (A_t) is the final amount
• (A_0) is the initial amount (principal)
• (e) is Euler’s constant (approximately 2.71828)
• (r) is the annual interest rate
• (t) is the time in years

Suppose you have $10,000 invested at an annual interest rate of 6%, compounded continuously for 3 years.

[A_t = $10,000 \times e^{0.06 \times 3}]

Calculating:

[A_t = $10,000 \times e^{0.18} \approx $12,213.48]

With continuous compounding, your investment would grow to approximately $12,213.48 after 3 years.

These examples demonstrate how different compounding frequencies (annual, monthly, and continuous) can lead to different final amounts, even with the same initial investment and interest rate. The more frequent the compounding, the higher the final amount due to the more frequent addition of interest to the principal.

Examples using the formulas

Let’s use the compound interest formulas to calculate the final amount for different scenarios.

Basic Compound Interest Formula:
The basic formula for compound interest is:

[A__t = A_₀(1 + r)^n]

Where:

• (A_t) is the final amount
• (A_0) is the initial amount (principal)
• (r) is the annual interest rate
• (n) is the number of compounding periods, usually expressed in years

Example 1: Annual Compounding:
Suppose you invest $5,000 at an annual interest rate of 8% for 5 years, with annual compounding. Using the formula:

[A_t = $5,000 \times (1 + 0.08)^5]

Calculating:

[A_t = $5,000 \times (1.08)^5 \approx $7,317.49]

So, after 5 years of annual compounding, your investment would grow to approximately $7,317.49.

Example 2: Monthly Compounding:
Now, let’s consider the same initial investment of $5,000 at an annual interest rate of 8%, but this time with monthly compounding. First, we need to adjust the interest rate and the number of compounding periods.

Monthly Interest Rate = 8% / 12 months ≈ 0.006667 (rounded to 6 decimal places)
Number of Compounding Periods (months) = 5 years * 12 months = 60 months

Using the formula:

[A_t = $5,000 \times (1 + 0.006667)^{60}]

Calculating:

[A_t = $5,000 \times (1.006667)^{60} \approx $7,374.49]

With monthly compounding, your investment would grow to approximately $7,374.49 after 5 years.

Example 3: Continuous Compounding:
In continuous compounding, we use the formula:

[A_t = A_0e^{rt}]

Where:

• (A_t) is the final amount
• (A_0) is the initial amount (principal)
• (e) is Euler’s constant (approximately 2.71828)
• (r) is the annual interest rate
• (t) is the time in years

Suppose you have $10,000 invested at an annual interest rate of 6%, compounded continuously for 3 years.

[A_t = $10,000 \times e^{0.06 \times 3}]

Calculating:

[A_t = $10,000 \times e^{0.18} \approx $12,213.48]

With continuous compounding, your investment would grow to approximately $12,213.48 after 3 years.

These examples demonstrate how different compounding frequencies (annual, monthly, and continuous) can lead to different final amounts, even with the same initial investment and interest rate. The more frequent the compounding, the higher the final amount due to the more frequent addition of interest to the principal.

Section 5: The Rule of 72

The Rule of 72 is a shortcut for estimating doubling time.

Need a quick estimate of how long it will take your money to double? Enter the Rule of 72. Simply divide 72 by your annual rate of return (in percentage), and you’ll get the approximate number of years it takes to double your investment. It’s a handy tool for quick calculations, though not entirely precise.

Example of how to use Rule 72.

The Rule of 72 is a simple and handy tool to estimate how long it will take for an investment or savings to double, given a fixed annual rate of return. Here’s an example of how to use it:

Let’s say you have an investment in a mutual fund, and it’s earning an annual return of 8%. You want to know approximately how many years it will take for your initial investment to double.

1. Start with the fixed annual rate of return. In this case, it’s 8%.
2. Apply the Rule of 72: Divide 72 by the annual rate of return. 72 / 8 = 9

The result, 9, represents the approximate number of years it will take for your investment to double at an 8% annual return rate.

So, in this example, if you invested $10,000 in the mutual fund with an 8% annual return, you could expect it to grow to approximately $20,000 in about 9 years.

Remember that the Rule of 72 provides an estimate and is most accurate for annual compounding. For more precise calculations, especially with different compounding frequencies or varying rates of return, you should use the compound interest formula.

Limitations and when it’s useful.

The Rule of 72 is a valuable tool for making quick estimates about how long it will take for an investment to double, but it does have limitations. Here are its limitations and situations in which it is useful:

Limitations:

1. Fixed Interest Rates: The Rule of 72 assumes a fixed annual interest rate. It doesn’t account for investments with variable or fluctuating rates.
2. Not Precise: It provides only an approximation. The actual time to double may vary slightly from the estimate, especially when dealing with interest rates that are not close to whole numbers (e.g., 8%, 10%).
3. Doesn’t Consider Compounding: The rule assumes annual compounding. For investments with different compounding frequencies (e.g., monthly or quarterly), the rule may not be accurate.
4. Inapplicable for Short Terms: The Rule of 72 is less useful for short-term investments or when you need precise calculations for a specific financial plan.

When It’s Useful:

1. Quick Estimations: The Rule of 72 is handy when you need a rough estimate of how long it will take for an investment to double without performing detailed calculations.
2. Mental math: It’s great for mental math and back-of-the-envelope calculations. You can quickly assess the potential growth of an investment during casual conversations or when making initial investment decisions.
3. Educational Tool: It’s a valuable teaching tool for introducing the concept of compounding interest and the time value of money to individuals who are new to finance.
4. Long-Term Planning: While not precise, the rule is suitable for long-term financial planning, retirement savings, and setting realistic expectations for wealth accumulation over several years.

In summary, the Rule of 72 is a useful, quick estimation tool for assessing the time it takes for an investment to double, especially when you’re dealing with relatively stable interest rates and long-term financial planning. However, for precise calculations and investments with varying rates or compounding frequencies, it’s essential to use more advanced financial formulas and tools.

Section 6: History of Compound Interest

Historical overview of compound interest, including its origins.

Delve into the fascinating history of compound interest, dating back over 4,000 years. Discover how different societies viewed compound interest, from its condemnation in Roman law to its widespread use in medieval times. Learn about Euler’s Constant (e) and its role in understanding the limits of compound interest.

Conclusion

In the world of finance, compound interest is your secret weapon for achieving financial prosperity. Whether you’re saving for retirement, investing in the stock market, or managing debt, compound interest can work for or against you. By understanding its principles and harnessing its power, you can pave the way to a more secure financial future.

So, what are you waiting for? Start exploring the possibilities of compound interest in your financial strategy today, and watch your money grow like never before.

Additional Resources

• Recommended Reading: “The Compound Effect” by Darren Hardy
• Investopedia’s Compound Interest Guide

Related Search Queries